『8÷2(2+2)=??』問題
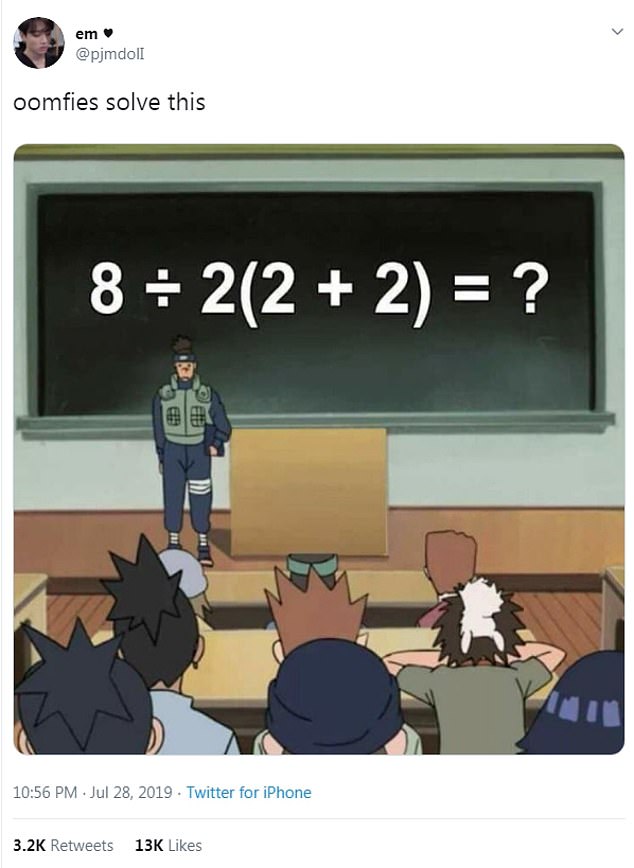
知ってます?
最近よく見かけるコレ。
大げさでなく、世界的に大論争が繰り広げられてましたが、ついに終止符が打たれたようです。
まず、
8÷2(2+2)
を解いてみてください。
凄くシンプルなこの問題。
別に、特別な公式をつかうでもなく見たまんま解くんです。
解けました?
では、一体何が起きているのかというと、
答えが2つに分かれるのです。
その答えは「1」と「16」。
しかも電卓でも答えが分かれる!

「16」派のこたえ
8÷2(2+2)
=8÷2(4)
=4(4)
=16
「1」派のこたえ
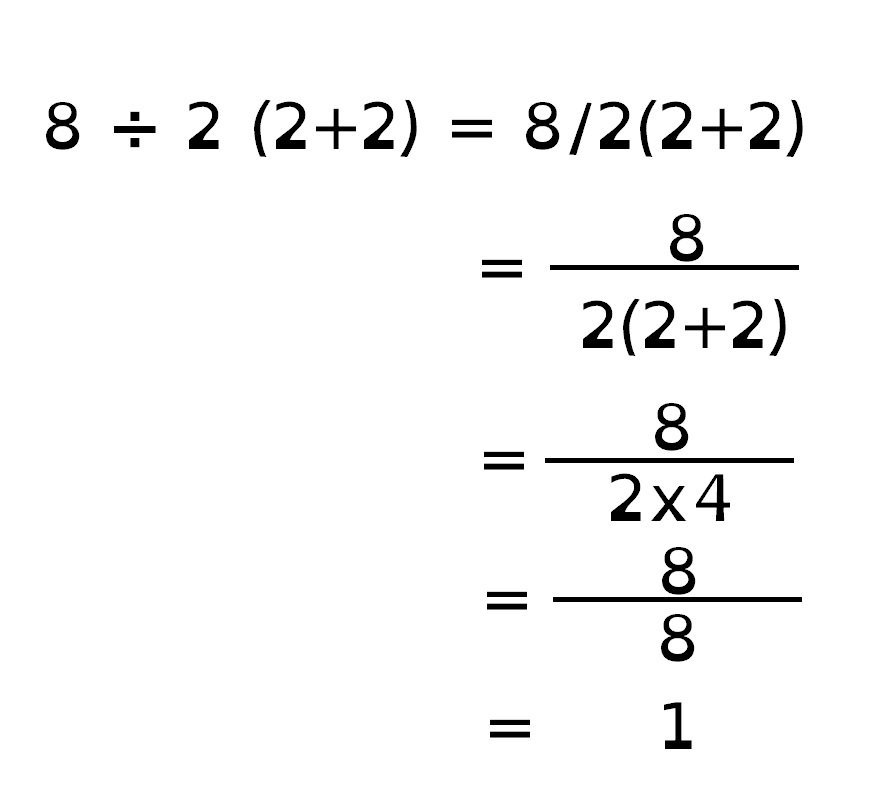
とりあえず、カッコの中を最初に計算するところまでは、どちらの立場でも同じです。
でも、そこからが違うんです。
(2+2)を計算して4になった後、2×4を先に計算するのか、
8÷2を先に計算するのかが答えの分かれ目となる。
「1」と「16」どちらが正解なんだ・・・。
こんな簡単な数式の答えが2つ出てくるという事態、ネット上では未だに論争しています。
そして、これに対してイギリスの数学者がついに登場し正解を発表しました!
それは・・・
『どちらも正しい。』
実はこれ、
その地域によって計算の順序の教え方が違うのも原因のひとつなんです。
アメリカではPEMDAS、イギリスではBOMDAS、カナダでは BEDMAS
が演算の順番として決まっています。
Pは、Parenthesesで( )括弧のこと。
Eは、Exponentsで指数のこと(ルートや2乗などの乗数)。
Mは、Multiply(掛ける)
Dは、Divide(割る)
Aは、Add(足す)
Sは、Subtract(減らす)
Oは Orderは累乗( 同じ数をいくつか掛けたもののこと )
なので、アメリカだと先にかけ算をするので答えは1になる。
イギリスやカナダなどでは、わり算を最初に行うので、答えは16になる。
というわけで、数学を学んだ場所によって正解は異なるんです。
そして、答えを発表した数学者が言うには、
『方程式が曖昧だから答えも曖昧になる』
とのこと。
確かに、なんでも曖昧な質問に対しては、
あいまいな答えが返ってくるものです。
こういうのがあるから数学っておもしろい。

